|
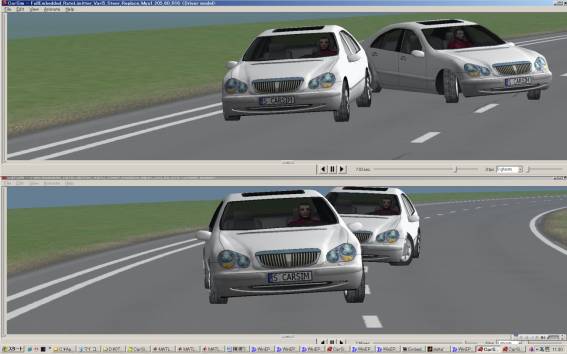
上の動画:数式Driver Moldelによる限界走行例、コーナリング中に二つの10cmの段差乗り越え。 1台はAbsorber制御 車両はCarSim (Mechanical Simulation社 ミシガン大UMTRI)
|
車の運転とDriver Model
このページ「車の運転とDriver Model」の目次
・運転対象を通して自分の動きを実現する
・車の運動モデル
・人の運動モデル
・我々の行為は無意識の内に行われる
・逆モデル
・運転を一言で言うと
・安全速度の実現
・滑らかな加速度制御
・感覚を備えた運動方程式: 感覚に沿った運動とは
・Weberの法則:人の運動逆モデル
・環境力場
・ハンドル捌き
・前輪後輪が発揮する横力の発生工程
・アンダーステアの強弱を決めるのは
・アンダーステア/オーバーステア補足
運転対象を通して自分の動きを実現する
自然現象を物理的に正確に把握する感覚が作り出す純粋な運動は自然現象。
”弘法筆を選ばず”、強アンダーステア車の対応不可能な突然急激なリバースステア時のハンドリングでも平然とこなす、どんな車でも運転してしまう弘法のような運転名人のドライバーモデルを作成しますが、その成り立ちについて簡単に説明します。
人馬一体の名人の乗馬を「鞍上に人なく鞍下に馬なし」と言う、馬は思い通りに走っているが、実は騎手の思いのまま走らされている 。
名人は運転対象を思いのままに操り、運転対象を通して自分の動きを実現させる。
自分の動きとは、環境(位置)ごとの安全(速度)を、感性に沿った(加速度)コントロールにより実現される動き。
自動車、航空機、船舶などの運転では、運転対象の操縦特性である物理的な入出力特性を練習によって習得し、運転対象と一体になってこれらを思うように動かす。
簡単に言えば環境に沿った速度のコントロールを感性に沿って滑らかに行うこと。
感性は車に加わる加速度の領域、安全は環境における速度の領域で、名人の運転の数式表現とは、感性に沿った加速度制御を行いつつ、環境における安全速度を実現する、加速度、速度および変位から構成される2次の微分方程式を求めることになる。
環境での安全速度を実現するには、加速度のコントロールによるそれ相応の積分時間を要し、秒単位の積分時間を遡った、先回りの見込み操作が必須となる。
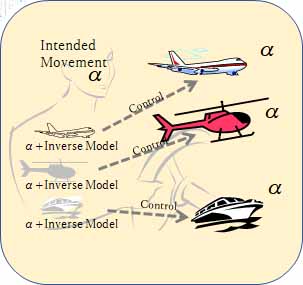
見込み操作は、結果である実現すべき(環境位置での速度)が先に与えられて、その実現のための今発揮すべき(力)を求める逆モデルで行われる。
運転行為に限らず人の行為は、練習によって脳内に獲得されるプログラム、内部モデル*1
により逆モデルの形で、実現べき見込んだ運動状態(位置X、速度V)から遡って行程(加速度α)を実行して行われる。
環境状況が練習通りなら獲得した内部モデルにより、見込んだ通りの意図した運動状態を正確に達成する。
練習で獲得する脳内モデルは次の二つの運動逆モデルからなる。
1 物理的入出力特性を表す運転対象の運動逆モデル(上図 Inverse Model )
2 運転対象の運動αを実現する人の運動逆モデル (上図 α )
一番目のモデルは運転対象を自在に操るコーナリングなどの機械的な車の運動を正確に操る運転技術を具現化するモデル。
「弘法筆を選ばず」、名人はどんな車を運転しても全く同じ車の動き実現できるが、車の特性によってその為の操作が車ごとに異なり、 ハンドル捌きなどに差異が出てくるので、
この名人のモデルの運転操作を計測して車両の操縦特性を定量的に評価することができる。
二番目のモデルは、人馬一体・人車一体の感性に沿ったヒトの生理に合わせた運動を具現化する、究極の上手い運転、感性に響く運転を実現するモデル。
中嶋悟の言う、楽器演奏に例えた感性に響く人車一体の運転を実現する部分。
フィギュアスケートの高橋大輔、宇野 昌磨 の華麗な滑りを見れば、 滑りには技術では表せない感性を揺さぶるものが無ければ本物とは言えないと言うこと、感性の大切さが理解されると思います。
運転の仕方によって乗っている人には様々な慣性力が働くが、この感性に沿ったヒトの運動モデルによる運転では、 無意識のうちに身体が反応して自然に筋肉が身体を支えるので、身体の揺れは意識されない。
そのモデルの具体的な形は次のようになる。
◎ 車両運動逆モデル:車を正確に操る
当然ですが教科書通りの運動方程式です。
操縦性をシミュレーションする場合、旋回時の前後輪での左右荷重移動を考慮した前後タイヤのコーナリングパワーKf、Krが必要。
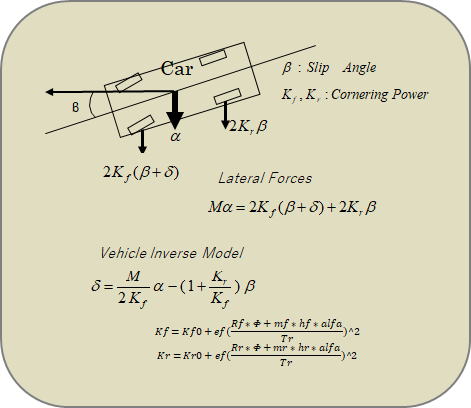
(δ:操舵角 、m,mf,mr:質量 Kf、Kr:前後タイヤのコーナリングパワ εf :荷重依存係数 α:横加速度 φ:ロール角
hf,hr:前後ロールセンタ高 Rf、Rr:前後ロール剛性 β:車体横滑り角(実車から得る))
◎ 人の運動逆モデル:意図を感性に沿った動きで実現する環境の先読み行動モデル
何億年もかけてDNAに刻み込まれた運動原理に従って安全運転を行う名人の運動方程式。
安全運転とは次々現れる環境毎にそこでの安全速度を実現して行くこと。
さらに名人の運転では、安全速度を実現する過程の加速度コントロールが人の感性に沿って滑らかであること。
交通環境に車両が進入すると、環境に応じた力が車に加わり、その力により安全速度が快適に実現されると考えると分かりやすい。例えば信号機(赤)があると自車の位置および速度に応じた力を信号機から車両が受けて、減速されて停止線で丁度速度ゼロになって止められる。
前方環境での見込んだ安全速度a/Cを実現する逆モデルとして、最も簡単な運動方程式:2次の微分方程式を下に示します。
α : x" = a - C x'
これは元東大生研名誉教授 故平尾収先生の考えに基づいて造った運動方程式です。
 先生は常々“事故原因は見込み違い”と言われてました。
先生は常々“事故原因は見込み違い”と言われてました。
この式は環境に応じて、先を見込んで車に働く力を算出するので、 環境と言う場の力を受けて安全運転を実現する見込運動方程式/環境力場の方程式になっている。
ITARDA(交通事故総合分析センター)在籍中に、先生が亡くなられる1年前まで世田谷のご自宅にお邪魔してご指導を頂きました。
さらにこの見込み運動方程式は、中嶋悟の「人車一体のヒトの感性に沿った運動」を実現する方程式でもあるのです。(後述1)
(後述2)
ひとの運動であることは後述しますが、これは先読みと同時に人の生理に沿った自然な筋肉運動で実現される見込み運動ですので、前後左右上下のどの方向にも適用出来ます。
例えば横方向のレーンチェンジ、旋回のコーナリング、上下の乗り心地に適用出来る。

ドライバモデルの数式には遅れに付いての項が有りません。
機械のの動きには遅れという表現は当たっていると思われますが、生き物の動作に遅れと言う表現は適切では無いと思っています。
それは、生き物は時間を遡って先読みで行動するからです。 強いて言えば、先行動作による時間のマイナスの遅れです。
意図の段階で、結果である積分時間を要する運動状態(位置・速度)を先読みして、結果に間に合うように先行して動作(加速度制御の行程)を開始して、
ジャストタイミングで意図した結果を達成してしまので、遅れとは無縁です。
イチローのバッティング、イチローのフェンスをよじ登っての捕球などをどう考えますか。
名人は間に合わないものには最初から手を出しません。
イチローがフェンスによじ登って捕球しているが、 捕球に失敗した場合、イチローに遅れがあったと解説するでしょうか。
バッティングの場合は、ピッチャーからの投球の球筋を予め見込んで、バットを事前に繰り出さなければ絶対打てないと思ってよいでしょう。
もっと極端な例として、サッカーのPK戦があります。 絶対間に合わない例ですが、キーパーは全能力を出し切って防ぎます。 それも相手が蹴る前に行動を起こします。 もしこれで防げなかったら、キーパーの取った行動に対して、見込み違いは指摘されても、遅れが原因と言うでしょうか。
平尾先生は、事故原因を「見込み違い」と主張されていましたが、この見込み違いの「見込み」は、生き物の行動の根元をなすものだと思っています。 生きものは見込み行動する、先読みですから遅れとは無縁のものです。
成熟した生き物は間に合わないものには手を出さない。 別な言い方では経験上自分の行動まで含めて分かっているものしか手を出せない。
我々の動作の本質は、練習したことしか出来ない、反対の手では歯も磨けない、しかし何事もやればやるほど上達し、やりきれば匠の域に。
動作は、先読みで意図する運動状態(速度・変位)を決めて 、この運動状態を実現する力(加速度)の行程を逆モデルの形で行う。
例えばカーブにさしかかると前方のカーブでの車の運動が先に決まって、
それを実現するためのハンドル操作を求める逆モデルを立ち上げる形になる。
動作時には練習で鍛えられた逆モデルが脳内で立ち上がり、身についた操作手順で必要な筋肉に指令を出す。
身についた動作は、脳科学で”手続き記憶“と言われ、徘徊可能な認知症でも失われないとされる、感覚も含んだ特別な記憶。
身についた動作は感覚も含めて無意識で一瞬に行われるので、どうやっているのか自分では分からない、どうやって歩いているのかさえ分からない。 見込み違いがあれば、よろけたり最悪転ぶだけ。 認知に障害があれば立て直しも困難。
筋肉系の準備から始める逆モデルでの動作を迷路で例えれば、慣れ親しんだ迷路の通過は、動作を意識する前に脳内で無意識の内にあっと言う間に処理されて、動作を意識した瞬間に筋肉系の準備完了でいきなり迷路の出口に立っている状態。
シミュレーションに必要なのは、”弘法筆を選ばず”と言うように、どんな車でも環境に合わせて常に同じ走行が出来る名人の運転モデル、 弘法の場合は同じ筆跡でも、筆によって筆使いの努力が異なるように、車両特性の違いはハンドル捌きに違いとなって現れる。
名人の運転については、元F1レーサー中嶋悟著「中嶋悟 運転の極意」三推社/講談社 によれば、運転を楽器の演奏に例えて、 カーブ云々の技術より大切なことは、人車一体のヒトの感性に沿った運転が出来ること。
この名人の感性に訴える運転の脳内プログラム(人の運動逆モデルと車両運動逆モデル)を推定して作成する。
注1: 内部モデル
(今水 寛 ATR 脳情報通信総合研究所https://bsd.neuroinf.jp/wiki/内部モデル)より
外部世界の仕組みを脳の内部で模倣・シミュレーションする神経機構である。ヒトや動物は、複雑な筋骨格系で構成される身体を、速く正確に制御できる。これは、脳の内部に、運動司令と身体の動きの関係を定量的に対応づけるモデル(信号変換器)が存在し、運動を実行する前に結果を予測したり、望ましい運動結果を実現するために必要な運動司令を予測することを可能にしているからと考えられている。このようなモデルは、身体の延長として機能する物体や
道具の入出力特性も反映する。また、
言語や
思考などさまざまな認知機能に関与する可能性も指摘されている。
AI ドライビングの物理
我々の行為は、脳内に保存されている感覚も含めた仮想環境モデルにより、
逆モデルの形で無意識のうちに行われる
いつの間にか乗れるようになった自転車、四苦八苦するも今ではすいすい乗れようになった車、でもどうやって運転しているのか自分では分からない。
我々の行動には無意識の部分が有り、この部分に行動の本質が隠れている。箸を使う場合、箸先の動きは意識するが、練習して身につけた指-手首-肘-肩の動きは無意識のうちに脳がやってくれているので、実際どうやって箸を動かしているのか分からない。
練習していない反対の手では、字も書けないし歯も磨けない、箸も使えない。 何事も練習、生き物は一生を練習で過ごす。
脳内にプログラムが作られていなければ、簡単な動作もままならない。
生まれて直ぐ訓練に入る動物たち、生まれた環境にすぐ慣れて生き抜けるよう、
デタラメから始める動物の赤ちゃんの何が起こっても動じない夢中になって遊ぶ姿/動作は見ていて飽きないし可愛らしい。
例えばマウスをクリックする場合
1.脳から指令が出て、
2.脳から指の先まで1m弱の長さの神経細胞を伝わって
3.指先の筋肉まで指令が届く
4.クリック
5.指先の感覚が神経細胞を伝わって
6.脳がクリックを感じる

このようにマウスをクリックするには、脳から指令が出て体が反応するのに、神経を通して指令が伝わるコンマ何秒かの時間がかかります。
実際のクリックは、クリックしようと思った瞬間に実現され、一呼吸遅れるはずのクリックの感覚/手応えも同じく瞬間に感じます。
触ってから遅れて脳に上がる絶対間に合わないはずのクリックの手応え/感覚、これも含めて思うより前に準備が出来ている不思議な形になっています。
自分の意思で始める時は、思った途端に寸秒の遅れなく即身体が動く、 しかし、”用意ドン“とか”始め“と他人から言われてスタートする時は必ずコンマ何秒か遅れて身体が動くことになる。 陸上競技の100m走では合図から0.1秒以内にスタートすると失格です。
字を書く場合は書こうと思った瞬間にペンが動いて、思った通りに線が引ける。
本当は脳から指令が出て、神経を経由して、指先の筋肉が応答する訳ですから、コンマ何秒か遅れて線が引けてもおかしくないのに、思った途端に手応え感とともに瞬時に線が引ける。
逆モデル
手応えも準備した仮想環境モデル、意図に基づく先行動作で遅れ無し
ただし練習して身についていることしか出来ない
これは私たちの行動が、感覚/手応えも含めた経験に基づいて身につけている脳内逆モデルで一連の行程を機械的に、 結果を時間的に遡って実現しているからです。
手応えも含めて全てが事前に準備され、無意識のうちに実行されている。
因果関係に沿って、こうすれば、ああなると言うのが順モデル、ああなるために、こうすると言う、結果が先にあって結果から遡ってその為の工程を実行するのが逆モデル、逆モデルは身に付いたノウハウのようなもの。
行動には必ず意図が先行する、例えば字を書く場合には、ペンを動かす前に、どんな字を書くのか、字の大きさ等が決まり、そのための指-手首-肘-肩の力を入れ方等の意図に沿った準備に既に脳は働いているわけです。
ペンを動かす前に
、結果として書かれるべき字を実現するための行為を、結果から時間的に遡った形で、
脳内では着々と進めている訳で、すなわち結果が先にあって、脳内で逆モデルが先行して感覚も準備して一連の工程を行っているわけです。
練習によって感覚も含めて全工程が逆モデルとして脳内にセットされているから、セットされた仮想環境の工程をひとつひとつ実施しているだけ。
覚えた迷路を逆から遡って入口から順に進むようなもの、途中は脳内で無意識の内に行われるので、
最初から迷路の出口に立っているようなもの。
その代わり動作環境も含めて練習して身に付いている事しか出来ない。少しでも脳内にセットされていた環境と実環境が違っていたら出口に行き着けない。
実行されるときは習い覚えた環境を想定して実行されるので、
呼び出された内部モデルに準備された仮想の環境が現実環境とずれている場合もあり、
たとえば段差の無いモデルが呼び出され、現実は段差があれば躓いてしまうと言うことにもなる。
のろまな我々生き物は全てこの練習によって身に付けた仮想環境逆モデルを、意図の段階で脳内に立ち上げて行動するので、
現実環境が読み通りであれば何事にもジャストタイミングの見事な動作が可能。
思うより先にプログラムを立ち上げて、正確で素早い行動を実現するこのシステムの欠点かも知れないことがあります。
最近話題の高齢者のブレーキとアクセルの踏み間違い、若い人にも踏み間違いは多いようですが、若い人では事故になりにくく高齢者では事故になりやすようです。
歩いたり楽器を演奏したりする練習して身体で覚える「手続き記憶」と言われる動作プログラムは、認知症でも機能すると言われています。
最近高齢者に仲間入りして自分でも気にしているのですが、何かをやろうとして手を伸ばした先を見て、あれ!、ということが若いときに比べて多くなりました。
実環境にそぐわない違ったプログラムを起動させてしまった場合、無意識での行為なので、実行後現実環境に戻り、
感覚がしっかりしていれば、そこで「あれっ!」となって、やり直しとなります。
認知症になると、脳内仮想環境で動いている状態を監視している現実の感覚がサボっているので、動作終了時でも現実環境に戻れず仮想環境のまま、テレビ等で見られるように、
店内に飛び込んでぶつかって止まっても未だアクセルを踏み続けて車が前後に揺れているいるようなことになるのでは。
私もすぐ近くで見たことがあります。
スーパーの駐車場で一つ置いた隣の駐車スペースで、前向き駐車の軽トラックが突然前進して、縁石を越えて前の立木に何回か頭をこすりつけた後、普通にバックして出て行きました。

しかし誰にも負けないたゆまない練習で獲得した逆モデルでも、プログラムは見込んだ運動環境条件に合わせて実行されるので、実行時の運動環境条件の読みに問題があれば、例えばピッチャーの投げる球筋の読み間違いがあれば、不適切なプログラムが呼び出されイチローでも打てないと言う事になってしまう。
日常経験することですが、物理的な状況に読み間違いがあっても、そのままプログラムは実行されるので、例えばスカを喰ったり、躓いたり、踏み外したり、みっともない形で終わります。 先行して脳内でプログラムが立ち上がってしまっているので、実行時に間違いに気付いても、手遅れで、つまずいて転ぶしか無い。
感覚がすべてを支配、仮想環境逆モデルは感覚で作られ、動作は感覚の監視下で行われ、感覚に評価される。 そして上手くいくかどうかは、モデル獲得に費やした練習量と、モデル実行時の物理的な環境状況を如何に正確に感覚が捉えているかにかかっている。
運転とは、環境ごとの”安全速度" を、感性に沿って"滑らかに" 次々実現すること
[弘法筆を選ばず]、どんな筆を使っても、筆捌きは異なるが、描かれるのは全く同じ美しい字体。
名人の運転で言うと、車の特性によってハンドル捌きは異なるが、車によらない全く同じ滑らかな運動を実現する。
弘法でも運転の名人でも、得られる結果は感性に委ねられる。
感性に沿った車の動きとは、安全な車の動きとは。
感性は車に加わる加速度の領域、安全は環境における速度の領域で完全に棲み分けられ、感性に沿った滑らかな運転と環境に沿った安全運転の両立は可能。
物理的に言えば、感性に合わせて変化する加速度の積分を経て所定の位置で安全速度を実現、と言うことになる。
名人の運転の数式表現とは、感性に沿った加速度制御を行いつつ環境における安全速度を実現する方程式を求めることになる。
脳内内部モデルで無意識のうちの行われる運転操作を具体的な形で表現するにはどうしたら良いでしょうか。 内部モデルの目指すところは明快で、“安全にそして快適に”です。
交通環境を”安全に”走るとは具体的にはどんな走りでしょうか。 ”快適な”とはどんな動きでしょうか。
元F1レーサー中嶋悟の運転に対する考え方を紹介させていただきます。
中嶋悟著「中嶋悟 運転の極意」三推社/講談社 から抜粋:
「僕にとってのうまい運転というのをひと言でいってしまうと、ドライバーとクルマが一体感をもって動いている運転ということになる。 ・・・コーナリングうんぬんということは、実は僕にとってのうまい運転の定義からすると、優先順位はいちばんにはならない。そういうひとつひとつの操作のうまいへたよりも、クルマと一体になって動いていることのほうが、僕はずっと大事なことだと思う。 ・・・ ひとつの楽器がテクニック的な意味でメチャメチャうまくても、なんとなくそれだけじゃうまい演奏とはいえないんじゃないかな?
・・・・・ 僕にとっての理想とは、クルマがもっと人間の感覚に忠実な機械として発展することを願うものだ。」
人馬一体の走りを「鞍上に人なく鞍下に馬なし」と言うように、中嶋悟の理想は車と一体になることだと言われ、元東大生研教授の故平尾収は車のことを人動車と言われ、 また自動車工学の権威の元東工大教授の故近藤政市は、人間と一体になってこれほど意のままに動く機械はないと、「私は、自動車は半分人格を持っていると考えており、自動車のことを半人間機械、半機械人間」と呼ぶことにしている」と言われていました。
中嶋悟は一体感からさらに踏み込んだ表現で「楽器の演奏に喩えて、技術も大事だがそれ以上に感性に響くようなことがもっと大事だ」と言われています。
動作を支配しているのは感覚、上達するほど際限なく微妙に動作を評価して、機械的には実現出来ないと思われる領域まで踏み込んで改善・上達、芸術の域にまで導く。
自動車の運動に関わる権威の方は、車は物理的な機械ですが、人が操るとその動きは人間そのものと言うことを言われているのだと思われます。 究極その動きは芸術の域まで高められると。
人車一体となって実現される精密機械より正確で滑らかな運動は、物理法則に従って走る車と、 それを心得て毎回巧みに運動制御する名人の運転によって成り立ちます。
車の物理モデルを脳内に形成して、その物理モデルと一体になってこれを毎回正確に操る名人の運転制御モデルが物理式で表現出来ると考えるのが自然な気がします。 すなわち人車一体の物理モデルを構成する人の運動モデルが物理モデルで表せることが分かります。
そしてその物理モデルが実現する動きは感性豊かな人の動きでなければならない。
環境に合わせた”安全速度” :位置と速度のコントロール、その場その場に合わせた安全速度を実現
運転者の一寸した不注意から思いもよらない取り返しのつかない重大な結果が引き起こされる交通事故。 違反種別で見ると漫然・脇見を含む安全運転義務違反による事故が全体の半分を占める。
運転に少し慣れれば、1トンから2トンもある運動神経の無い鉄の塊を、自分の運動神経を頼りに、街中を秒速10m以上の速度で何の不安も感じないで走らせてしまい、ついでに美人が居れば脇見をしてしまう。 運転者に美人は見えるが危険は見えない。
“漫然運転、でも脇見だけはしっかりと”。
一寸した不注意が原因なら、ほんの少しの注意で事故は防げる。
人間には、このほんの少しの注意が難しい。
機械には簡単かも知れない。
美人が脇を通っても機械は見向きもしない。
安全な速度まで減速するのを機械は嫌がらないし、最悪止まってしまうのを厭わない。
人間なら漫然・不注意、脇見になるところを見落とさずにちゃんと前を見て、機械の判断で適切な速度を決定し、 人間なら「まーいいや」とそのままの速度で行ってしまうところを、 しっかり速度を落としてもらうと言うのが、現在期待されている機械による一寸高度な安全運転支援である。
さらに機械を超えて相手との意思疎通を考慮した、安全運転の本質である”常に譲る”のレベルまで行けば、言う事ないですが、ちょっとむりかな?
無理ではありません、正確な状況判断の速さに依存します。 常に相手より速く状況判断が出来れば、常に譲る側に立つので、譲る行為は相手の意思を確認せずに可能となります。 相手の意思にかかわらず、最悪でも止まって待つ形になります。
安全運転支援ではセンサー次第でヒトのつまらないミスによる事故は確実に防げるので非常に有益です。
ただ、秒速10m以上のスピードで動いている1トン以上の鉄の塊が、突発事態では物理的に止まれるはずが無く衝突は必然で、 安全運転支援装置による自動運転でも事故防止は難しい。漫然運転の車や歩行者などの混在する現在の交通環境のままでは、 ヒトの運転と比べて安全状況はあまり変わらないような気もします。
交通事故は誰にでもどこでも平等に起こるのではなく、物理的な衝突の可能性を潜在させている危険な環境に接して、これを見抜けなかった運転者がいると確率的に発生する。
事故の発生要因
・環境に潜在危険
・潜在危険に気がつかない運転者がそこを走って
・量的因子
普通は潜在する危険が有っても、その危険に気が付かないし事故も起こらない、 毎日同じ道を同じように走って、たまたま子供が飛び出して偶然事故になるので、本人も自分の運転に原因があるとは思わない。
安全な運転者はどうしているのか?
「車は急に止まれない」、昔は子供の飛び出しが多くよく言われたものです。
車など飛び出しの危険のあるところでは、事前に速度を落として走っているので、万一飛び出しが有っても、普通の運転で対応可能で飛び出しにならない。
さらに言えば余裕を持った滑らかな速度コントロールで何ごとも無かったように走れることが望まれる。
自分の身体は運動神経でどうにかなると考えているかも知れないが、1トン以上の鉄の塊の車には運動神経が無い、車と一体になって動き回る場合は運動神経では全く間に合わない。 大切なことは、先を読んで事前に落とす速度を決める、そしてそこに達したらその速度が自然に実現されていること。
人動車の行動をモデル化するとき、通過環境ごとの所定の位置で所定の速度が実現されること、このことが重要になります。
平尾収は、運転の本質を「先を読んだ見込み動作」として、事故原因は「見込み違い」と言われていました。
例えば追突事故は脇見が原因と言いますが、脇見は誰でも普通にすることで、これを原因とするとそこいら中事故だらけになってしまいます。
脇見もせずに真剣に前ばかり見ている運転には、それこそ心配で乗っていられません。
先を読んだ見込み動作とは、通過する環境に応じた安全速度を先読みし、その環境に適合した安全速度を道路に沿って現れる環境ごとに次々と実現すること。
積分時間を要する変位(位置)および速度の実現には時間を要する。 これをタイミング良く行うには、逆モデルによる先読みの見込み動作で対応する。 変化も含めて環境を先読みし、予め練習で獲得している逆モデルによる動作でこれに対処する。
感性に沿って"滑らかに” :加速度コントロールは感性に合わせて
環境を前にして、(運動に)先立って生じる運動意図を実現する人の運動制御式は、 環境での運動が先に決まる環境駆動の逆運動モデルに成っている必要があり、
中嶋悟はさらに、この運動がヒトの感性に響くことを求めている。 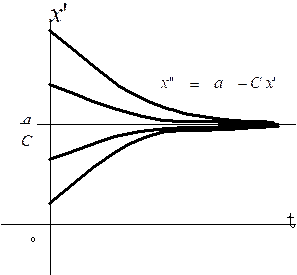
一般的には目標速度を実現する最も簡単な微分方程式は
x"
= a - C x'
初速の如何に関わらず速度 a/C に収束する運動を表す。
さらにこの微分方程式による加速度運動が人の感性に沿っていることが、別途感覚の法則から保証されるので、
結果的にこの式が安全速度を快適に実現する人の運動逆モデルとなる。
感覚を備えた運動方程式: 感覚に沿った運動とは
人間も大自然の一部として進化:感覚は大自然の物理現象の代弁者
我々は感覚で物理量を正確に把握している。 スカを食うと言う言葉がありますが、ものを持ち上げる場合も、事前にまず目で重さを推定し、それに見合う力を出して持ち上げる必要がある。 思った通り持ち上がったかどうかも感覚で確認している。
運動と感覚の関係は重要で、視覚、聴覚、触覚、運動感覚、力覚などの感覚が正確に物理量と1対1に対応していると思われる。
人も大自然の一部、何億年も前から、大自然の中で進化し続けてきた。 餌をとったり、捕獲者から逃げたり、運動に関わる視覚、聴覚、力の感覚などは、物理的な現象と物理的な運動能力と密接に関係して進化してきたと思われる。
感覚と大自然の物理的な運動法則が正確に対応していなければ、ここまで進化し続けてこられない。
感覚は生き物に備わったものだが、大自然の物理的な原理そのものと考えられる。
我々は、匠の物差し、美の原器を持たされて生まれてくる、音痴でもベートーベンが分かる。 感覚は生まれたときからプロ、素人でも一瞬でプロの技を見抜く、しかしやってみればぶざま。
大自然の摂理が何億年にも渡って刻まれた虎の巻を授かっている、何もしなければ、虎の巻は埃を被ったまま。
努力(行動)すればするだけ幾らで努力(行動)すればするだけいくらでも開示される。
すべて生まれてからプログラムされる、赤ちゃんの行動を見ればすぐわかるように、習うより慣れろ、どんなことでもその環境で自分でやってみて習得しなければ何も出来ないように仕組まれている。
そして、やってみれば、全知全能の神がコーチ役を引き受け、動きを見守りプログラムを修正、次の機会によりリファインした動きを実現する。 コーチの正体は、自然界の美しさ、プロの技を一瞬の内に見抜く、自分自身の感覚。 トライする度に洗練される運動は、感覚の中に秘められた究極の運動に限りなく近づく。
 運動は、敵から逃げたり餌をとったり命に関わる重要な行為なので、これに関わる視覚、聴覚、触覚、運動感覚、力覚などの感覚は正確に物理量と1対1に対応している必要がある。
運動は、敵から逃げたり餌をとったり命に関わる重要な行為なので、これに関わる視覚、聴覚、触覚、運動感覚、力覚などの感覚は正確に物理量と1対1に対応している必要がある。
この感覚の世界を物理量の世界に変える手段は19世紀の生理学者
感覚と物理量との対応関係を示す(ウェーバーの法則)
ΔS/S = C 一定 、この式は感じることが可能な最小の物理変化量が現在値に比例することを表しているが、
放射性物質の崩壊、熱せられた物体の冷却など自然界の非常に基本的な現象と同じ式の形をとる。
大自然と一体の感覚も単純な単なる物理法則に従った自然現象としての存在になるのでは。

(ウェーバー))の法則の物理刺激量Sとして
ΔS/S=C 一定
運動中の身体が受ける力(mx")を考える。 Δt を力の変化を感じる短い時間とすれば、ΔS=dS/dt*Δt ここに S=mx" となるが、このΔS、S をWeber比の式 に適用すると、身体が受ける力(mx")の感覚が作り出す3次の微分方程式が得られ、これを積分して2次の微分方程式 x" =
a - C/Δt x' を得る。
感覚が目指して求める究極の運動 x" = a - C x' が得られる。
感覚の法則、Weberの法則から導かれたこの式は滑らかな運動を保証するだけでなく、さらに、予想された通り、前述の微分方程式で示した速度を見込む運動の逆モデル(運動制御則)と同じ微分方程式になっており、環境に合わせた見込み運動を行う。
この式を変形
x" = a - C(X,V) x'
ここに、(X,V)>が環境での運動状態。
この式はこの運動状態(X,V)を感覚に沿って滑らかに実現する。 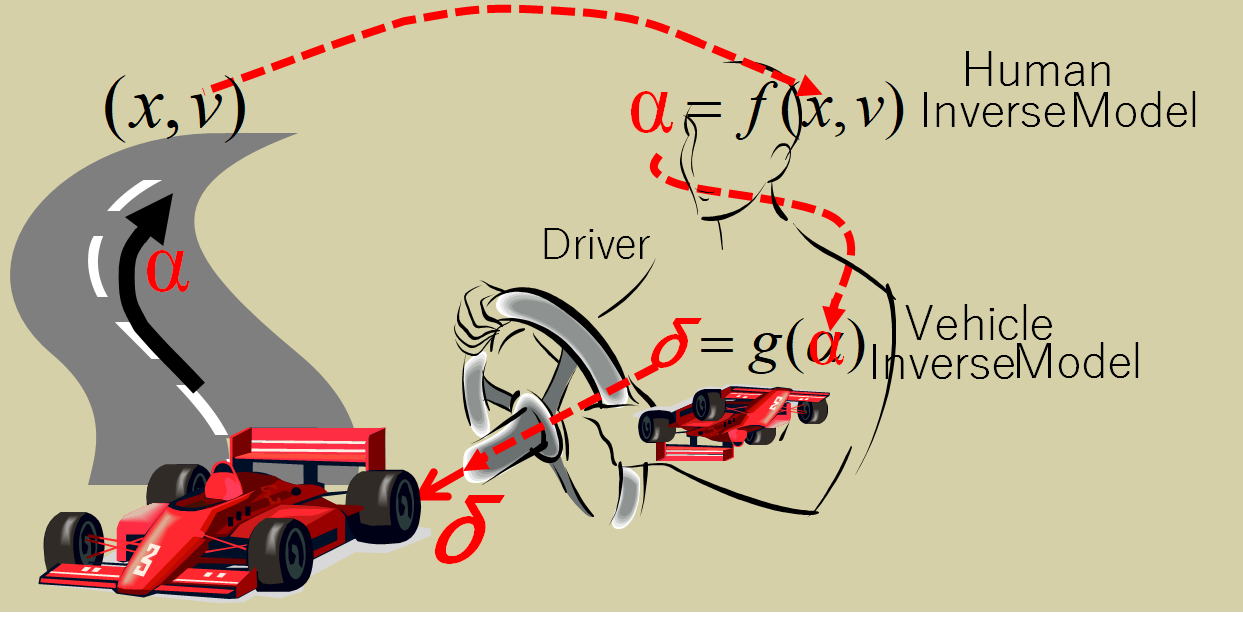
人の運動逆モデルでは環境に対応する取るべき運動状態(X,V)が先に決まり、それを実現する運動αを行う運転操作δを車両運動逆モデルによって求め、 その求めた操作δを車に行って、思った運動αが車の運動αとして実現され、最終的に環境での運動状態(X,V)が車で実現される。
先読みによって定めた運動状態を、車の滑らかな動きで実現するには、「その運動状態を実現する運動(加速度)を算出する”人の運動逆モデル”」 および 「算出した運動(加速度)を車の動きで実現するステアリング操作量を求める”車両運動逆モデル”」の両方が必要。
上の図で、f(X,V)=α が人の運動逆モデル。 V(α)=δ が車両運動逆モデル。
(X,V) は環境での取るべき運動状態で α がそれを実現するヒトに快適な加速度パターン。 操作δ は車両で α を実現する操舵角。 f(X,V)=α はWeberの法則から求まった x" = a - C(X,V) x' の加速度運動を示す。
環境力場:交通環境を安全快適に走り抜けるよう車に働く環境力 具体例はこちら
環境が車両の運動を支配する。
運転者は前方環境での通過の安全速度を先読みし、その安全速度を実現するよう、車両の運動をコントロールする。
車両から見れば環境に入り込むと、環境から力を受けて、所定の速度に落ち着くように力のコントロールを受ける。
人の運動を支配するのは環境で、環境ごとに力の場が張られ、車両は環境力場に沿って運動するので、
見込み運動方程式=環境力場の方程式 と考えると、
人による車両の運動が物理的に理解し易くなります。
所定の速度を実現するもっとも簡単な微分方程式は x" = a - C x'
この式は物体が水中をまっすぐ進む時の運動を表しています。a は推進力を、 C は水による抵抗度合い/減衰係数を表しています。
魚で例えれば a が尾びれで C が胸びれです。 魚はこれで水中を自在に泳ぎ回ります。
車の動きでは、C による減衰力 Cx’ が環境に応じて車に働く仮想的な力、環境力が車に働くと考える。
赤信号で車が止まるのは、車を止めるような力 Cx' が信号機から車両までの距離、車両の速度に応じて働いていると考える、前の車に追いついても車間を詰めないのは、前の車との自車の相対位置および自車の相対速度に応じた力Cx' を受けて適正車間を維持すると考える。これらの力を環境力と呼ぶことにする。
車の直前に飛び出しがあれば、飛び出したものが環境力を瞬時に張ることになり、車速と飛び出し位置によっては強力な力を受け、急制動となる。
この環境力を張って、滑らかに安全な速度を物理的に実現する力の場をつくる。
具体的には、(安全速度 V、実現位置X )の環境に、 車両の 位置 x 速度 x で進入してきた車両に働く加速度 を決める関数を式(1)で表わし、 これを環境力方程式と名付ける。
x" = a - C (x,x',X,V) x' (1)
この式は環境(速度規制、信号機、障害物など)が作用して、環境に侵入する車に対して侵入時の走行状態(速度x'・位置x)応じて mx" の環境力を作用させると見なすことが出来る。
安全速度V (実現位置X )の環境に速度x' 位置x で進入してきた車両に働く加速度x"を決める関数になる。
C---> C(x,x'X,V)
中島悟の、楽器演奏に例えた上手い運転 “感覚に忠実な滑らかな運転” は、
感覚の法則から導かれる運動方程式 x" = a - C x' が行う加速度運動で実現される。
平尾収の言う事故原因は“見込み違い”、言い換えると事故を防ぐ安全運転の“先読み運転”、 すなわち前方環境での安全速度を実現する運動方程式も x" = a - C x' である。
上手い運転の加速度コントロールと安全運転の速度コントロールが、全く同じ運動方程式で実現されることになる。
物理的には速度は加速度コントロールで実現されるので、滑らかな上手い運転なら安全運転であると言うことになるが、 雑な加速度コントロールでも安全速度の実現は可能なので安全運転なら上手い運転とは言えない。
この運動方程式 x" = a - C x' は数学的には、初期条件として如何なる速度が与えられても必ず、一定速度a/Cに収束する。
環境に応じた安全速度を次々実現しながら走るのが安全運転、前方環境の安全速度をa/Cで与えれば、この式はこの与えられた安全な速度a/Cで走る運動を実現する。
この安全速度を実現するための加速度のコントロールは、この運動方程式が自動的に行うが、この式は感覚から導かれた式と一致しているので、その加速度コントロールは感覚に忠実な滑らかなものとなることが保証されている。
この運動方程式 x" = a - C x' は平尾収の安全運転を、そして中嶋悟の滑らかで快適な匠の運転を同時に実現する人の運動方程式となる。
滑らかな運転には正確な先読みは必須で、運転の滑らかさは正確な先読みの結果、すなわち安全運転を保証する、それを実行している中嶋悟の150万キロ無事故も頷ける結果。
中嶋悟は、誰でも人車一体自分の手足のような感覚で、自由に安全に走れる車の実現を望んで、
「僕にとっての理想とは、クルマがもっと人間の感覚に忠実な機械として発展することを願うものだ」と著書「中嶋悟 運転の極意」の結びとしています。
車両モデルが行うハンドル捌き
前輪後輪の役割
アンダーステアの強弱・操縦性を決める仕組み
*以下参考(定常円旋回)
周波数応答によると、アンダーステアが強いほど安定した挙動を示す。
操舵の効き具合を見るため、アンダーステア車の操舵に対する車体の動きの周波数応答を機械的に調べます。
(車両モデルはKf,Krの値が固定された運動方程式で、計算は Mathematica)
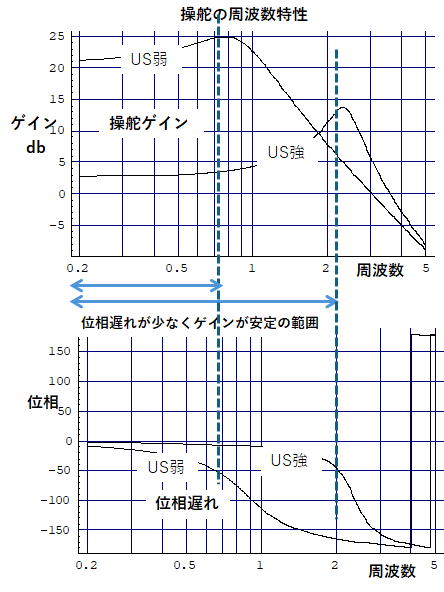
左にアンダ-ステアのレベルが異なる2台の車両(フロントコーナリングパワー1割増しの弱US車、リヤコーナリングパワー2割増しの強US車)の ”前輪舵角に対する車両横滑り角”
の周波数応答のゲインおよび位相遅れのグラフを示す( ”横加速度/前輪舵角”の応答も殆ど同じです)。
ゲインが高く舵が良く効くが周波数帯域が狭いのが弱アンダーステアのグラフです。
ゲインが低く舵の効きが悪いが周波数帯域の広い範囲で安定しているのが強アンダーステアのグラフです。
アンダーステアが強いほど舵の効きが鈍く操舵に対して車両の動きが安定なことを示しています。
しかしアンダーが強ければ良いかと言うとそうではなくほどほどのところがある。
*ここまで参考(定常円旋回)
動的にはどんな車もUSの強弱レベルに応じたリバースステアが起こり、高速サーキットでのレースで見られるようにUSレベルの強い車の場合プロでもスピンしてしまうことがある。
USの強さがあるレベルを超えていると、アンダーが強い分無理してかなり切り込んだ状態から起こるリバースステア時には、 車体の回転に連動して前輪の舵角もその回転角分増加し、
それに対する修正操舵が舵のゲインの低さも相まって、相当量ステアリングを逆ハン方向に素早く戻す必要があるが、腕力が追いつかずプロでもスピンしてしまう状態が発生する。
このリバースステア時のハンドル捌きは、人では腕力が追いつかないので、人の運転を通して明らかにすることが出来ません。
腕力の制限無しで人と同じ運転、どんな車に乗っても同じ運転が出来る”弘法筆を選ばず”の弘法のような名人の運転によるシミュレーションで、
弱アンダーステア車から強アンダーステア車のリバースステア時のハンドル捌きを具体的に示します。
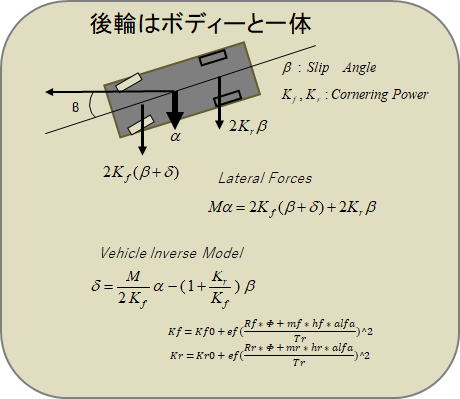
運転する車両の入出力特性式は下の図に示すとおり、教科書通りの運動方程式を当てます。
車が 行うべき運動がαで、このαを入力して出力である操舵輪の角度δを出力する。 横滑り角βはシミュレーション中の車両の走行中のデータを使用します。
アンダーステア・オーバーステアの操縦性をシミュレーションする場合、アンダーステアの強弱を決定する旋回時の前後輪での左右荷重移動を考慮したKf、Krが非常に重要です。下記する式で算出した値を使用します。
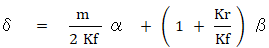
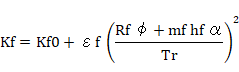
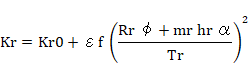
(δ:操舵角 、m,mf,mr:質量 Kf、Kr:前後タイヤのコーナリングパワ εf :荷重依存係数 α:横加速度 φ:ロール角 hf,hr:前後ロールセンタ高 Rf、Rr:前後ロール剛性 β:車体横滑り角(実車から得る))
このシンプルな車両運動逆モデルで行うハンドル捌きは、後輪が背負う車体の回転のコントロールを介して行うかなり込み入ったものになります。 旋回時は後輪が適切な角度取って踏ん張りますが、重い車体を背負っていて前輪のように自在に素速く所定の角度を取れません。 しかも前輪と違って自分では動けません、車体の回転頼みです。
下手な運転の車でも、この逆モデルを組み込んでおけば、走行中の運転者の意図(速度・変位)を含み持っている加速度を計測すれば、 この逆モデルだけで難しい横滑り自在の ステアアシスト をすることが可能。
前輪後輪が発揮する横力の発生工程がどうなっているのか考えて行きます。
大事な点は操舵に対して一呼吸遅れて車の運動が開始されると言うこと。
車体と一体のリヤタイヤが進行方向に対して横滑りして、初めて車体にコーナリングフォースが発生する。すなわちフロントタイヤの操舵に対して、重い車体が向きを変え終わって初めてリヤタイヤにコーナリングフォースが発生する。
通常の運転におけるコーナリング時の、減速しながらコーナーに入る時の遠心力の変化の過程、 および直線運動に戻るときの加速 から直線走行に移る遠心力の変化の過程が肝心です。
しかしこの場合微妙なコントロールはステアリングと言うよりアクセルとブレーキのコントロールにゆだねられる。 この場合ステアリング操作は脇役で、役割が分かりにくい。
ハンドリングが主役のきつめの横滑りが発生するようなコーナリング時の極端なハンドリングについて考えます。

ステアリング操作による力加減の特徴は、重い車体の回転を介して行う間接的なコントロールになると言うことです。
ハンドル捌きによる力のコントロールが生じるのは、一呼吸おいた動きの鈍い車体の回転後
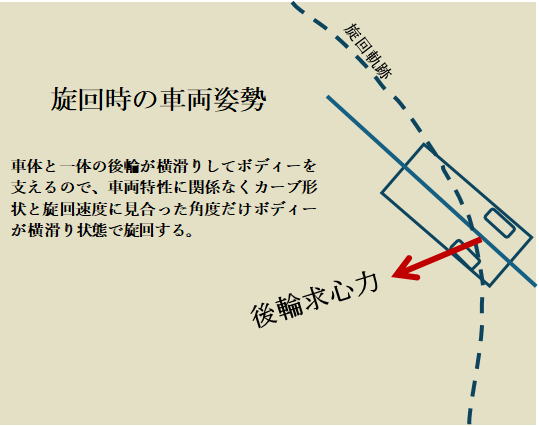
ここではステアリング操作によってタイヤに発生させる力のコントロールの工程について調べる。 車体を背負った後輪の横力がキーになる。大切なのはボディーと一体の後輪が車体を支えていると言うことです。
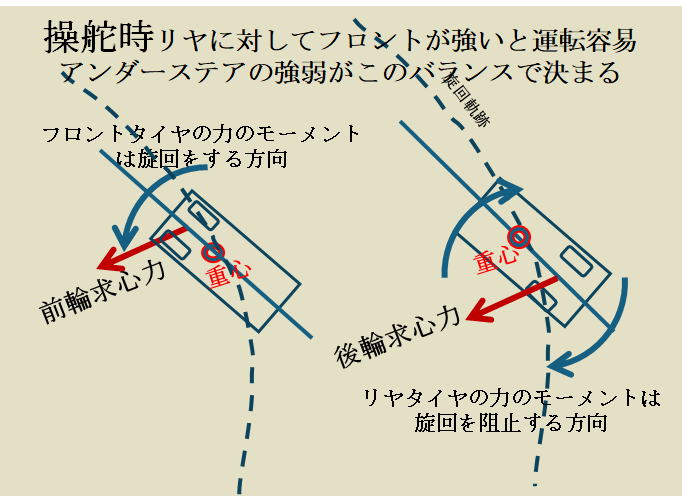
左の図に左旋回中の車両の姿勢を示すが、リヤタイヤが横滑りしないと車体は支えられないので、激しい運転でも温和しい運転でもどんな運転でも旋回中はリヤタイヤと一体の車体は必ず図のように横滑り状態になります。
車体と一体構造のリヤタイヤが車体を支える役割を担い、フロントタイヤの役割はフロントタイヤの力でこの車体の向きを自在にコントロールすること。
リヤタイヤはフロントタイヤの力によって一呼吸遅れて車体と一緒に向きを変えて、車体をささえる力を発揮し意図した旋回が成立する。
フロントタイヤを操舵して車体を進行方向に対して必要な角度を持たせ、横滑りするリヤタイヤの軸方向の摩擦により、車体に横向きの力を発生させる。 カーブ旋回に見合った求心力およびヨーレートを発生する所定の車体(リヤタイヤ)の横滑り角が得られれば、 そのリヤタイヤの発生する力にバランスさせた力をフロントタイヤが発生するようにフロントタイヤの向きを合わせる。
スーパーマーケットでの買い物時のカートを操るのと同じ。
左の下の図に、旋回に関わるフロントとリヤのお互いにせめぎ合で働く相反する車体に働く回転モーメントを示す。
操縦性を決めるアンダーステアの強弱レベルは、操舵を加えた時の車体を支えるリヤタイヤの踏ん張りモーメントと、 その踏ん張り力に逆らって車体を回転させるロントタイヤの発揮するモーメント、この二つのモーメントのバランスで決まります。
フロントの回転モーメントが強いほど舵が効くので自在の運転が可能で、 リヤの回転モーメントは舵を戻す方向に働く力になるのでこれが強いと思い通り舵が切れないことになる。
しかしフロントの力で舵が決まって所定の車体の回転が得られた後は、リヤは車体を支えるので弱いと旋回能力が落ちてしまう。 フロントとリヤのバランスの落としどころでアンダーステアのレベルが決まる。
進行方向に対して角度を持ったリヤタイヤが横滑りして発生する求心力は、 同時に車体の向きを元に戻す方向の回転モーメントを発生させるので、操舵輪はこの力とのバランスにより、 車体に旋回に必要な求心力を得ると同時に車体に働く回転モーメントをコントロールして旋回に沿ったヨーレートを実現する。
アンダーステアの強弱を決めるのは、前後サスペンションでの左右のタイヤ間の荷重移動量の差異
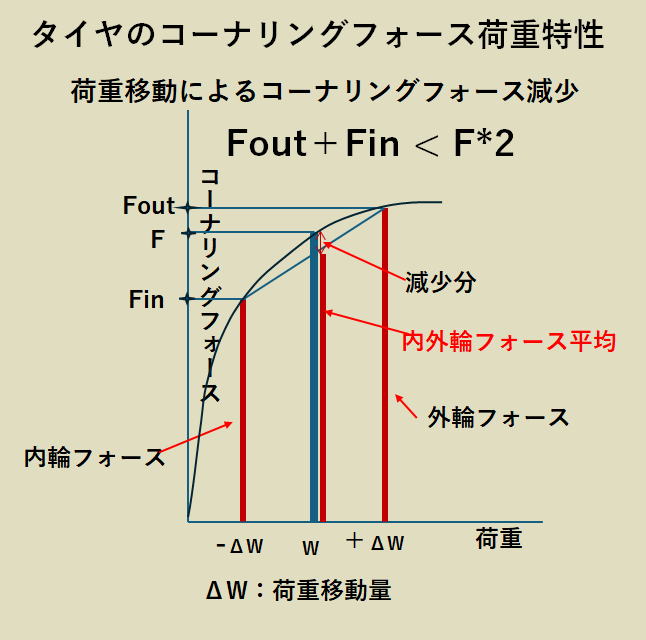
前後のタイヤのコーナリングフォースの強さの違いによって舵の効き具合が変わりますが、 前後での強さの違いは前後サスペンションの剛性配分の違いによって、 前後での旋回外輪への荷重移動量が異なるために生じます。
サスペンションの剛性が強いほど踏ん張るので、左右の荷重移動量が大きくなります。
荷重移動によるコーナリングフォースの減少については左の模式図を参照ください。
横軸はタイヤに加わる荷重、縦軸はその時のタイヤが発生するコーナリングフォース。
ロール剛性が強いと旋回時の内輪から外輪への荷重移動量が大きくなります。 加重に対するコーナリングフォースの形が上に凸になっているので、荷重の移動量が大きい程その分コーナリングフォースが減少します。
フロントとリヤのロール剛性配分によってアンダーステアのレベルが変わります。剛性がより強い側で荷重移動量が大きくなり、コーナリングフォースはその分大きく減少します。
フロントがリヤより剛性が強いほど、フロントでの左右輪の荷重移動が大きいことによるコーナリングフォースの減少がリヤより大きくなることによりアンダーステアが強くなります。
フロント側のロール剛性を弱くすると、ロール時に左右の荷重移動が少なくなりフロントでのコーナリングフォースが落ちないので、アンダーが弱くなり車体のコントロールが楽になり、ラリーのような走りが容易にできます。
リヤのロール剛性を弱くするとフロントを弱くした場合の逆で、リヤでの荷重移動が少なく、リヤタイヤのコーナリングフォースが維持されてアンダーが強くなり、 無理のかかっていないリヤタイヤに余裕が生まれているので、その分駆動力を駆けることが可能になり、アクセルコントロールによりスピードサーキットでの高速旋回が可能となります。
ただし、アクセルの微妙なコントロールとステアリング操作の合わせ技によって、アンダー分を使い切ってオーバーステア寸前までのニュートラルステア状態に持って行って走るのは簡単ではない。
下の動画と写真はレーンチェンジの時のハンドル捌きを示す。前輪の動きとリヤタイヤに働く力と車体の動きを見てください。車両はCarSim。
ドライバーは冒頭に記述の数式ドライバーをMATLAB/Simulinkで記述したもの。
ハンドル捌きのドライバーモデルは3章”横方向の運転のモデル例”に記載。
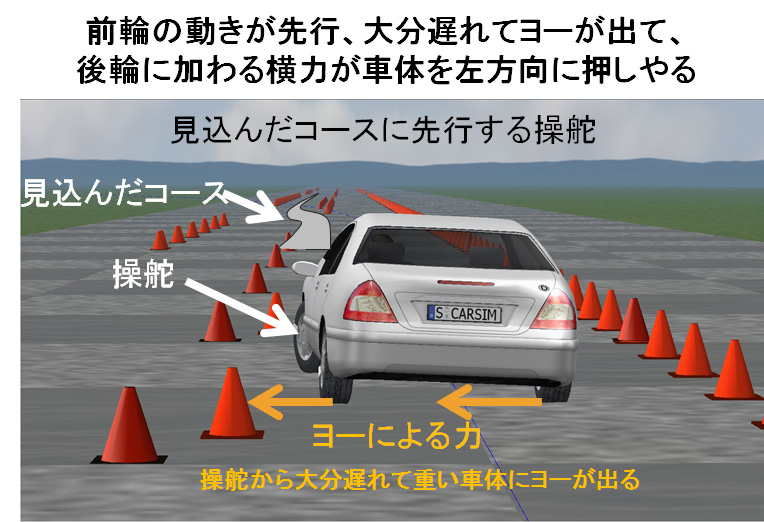
フロントタイヤを含む操舵系がこの車体(リヤタイヤ)の向きを自在に変えることになるが、 時間遅れの大きい重い車体の回転運動を介在するので、操舵によるリヤタイヤに発生させる力加減はかなり難しい。
アンダーステア・オーバーステアについて補足

動的にはアンダーステアの状態とオーバーステアの状態の両方を行ったり来たりする。
よほどアンダーステアが強くない限り、どんな車もリバースステアしオーバーステア状態になる。
アンダーステアが強いほど急激にリバースし、 弱いと穏やかにリバースする。 アンダーステアが弱いとオーバーステア状態に自然に移行して、リバースが意識されないほど。
フロントもリヤもそれぞれ大切な働きをするが、各々の発生する力のバランスで操縦特性が決まる。
旋回ロール時に前後サスペンションのロール剛性配分に応じて、前輪および後輪において旋回内輪から外輪への荷重移動が生じ、 剛性配分の大きい荷重移動量が多い側でコーナリングフォースの減少が大きくなり、この前輪後輪に生じる力のバランスで操縦特性が決まり、
リヤでの荷重移動が大きい弱アンダーステアの場合はリバースステアに容易に移行する。
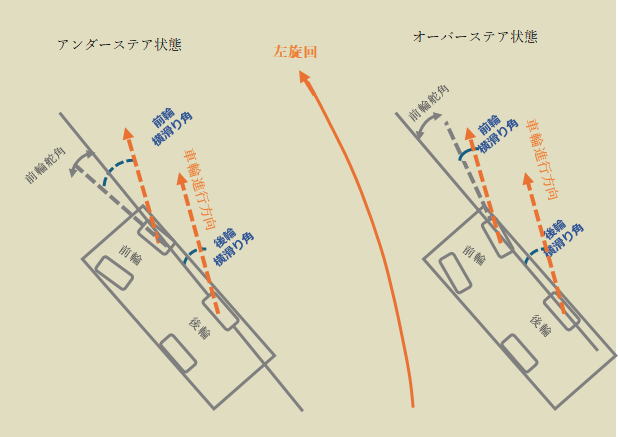
前輪での荷重移動量が後輪より大きいときには、言い換えるとフロントサスペンションの剛性配分がリヤより大きい場合、
前輪の求心力がより減少してアンダーステアが強くなり、左図の左側の車両のようにコーナリングフォースを上げるため前輪を切り込んで車体(後輪)に対して前輪の横滑り角を大きくした状態で旋回する。
逆だと右の車両のようにアンダーステアが弱くなり、前輪の横滑り角を減らして、車体(後輪)より横滑り角を減らしてリバースステアに移行しやすい。
アンダーステアが強いと感じた場合は慎重に運転する必要があり、無理に切り込むと突然右の車両のような状態に移行するリバースステアが起こり、 クルマは物理的に旋回可能でもヒトのステアリング操作の腕力が足りずプロでも最終的にスピンに至る。
サーキットで行われるスピードレースではプロのドライバーがスピンしている光景がよく見うけるが、スピードを競う場合はアンダーが強い方がリヤの横滑りが少なくコーナーでのスピードが落ちにくく、
さらに余裕のある後輪に駆動がかけられ早く走るには有利なため、リバースが起こる危険をおかしても、
高速サーキットでのスピードを競うレーシングカーは、アンダーを強めに設定していると思われる。
強アンダーステア状態は上の左側の図に示す状態で、リヤのコーナリングフォースに余裕があってフロントが無理して切り込んでいる状態。 リヤタイヤの摩擦力に余裕があるこの状態で、余裕分の範囲でリヤに駆動力を駆けるとコーナリング速度を上げることが出来る。
しかし駆動力をかけすぎて余裕分を使い切ると、右の図のように逆ハン状態にまでなってしまってコーナリング速度を維持できなくなる。逆ハン状態になる手前のニュートラルステア状態になるまでリヤタイヤに駆動力をかけることが可能。
ポール・フレール著「ハイ スピード ドライビング」二玄社 の中に、ステアリングとスロットルの微妙な操作によりニュートラルステア状態に達する手前で最大のコーナリング速度が実現できると記述がある。
そしてジャック・ブラバムが微妙なスロットル操作によりニュートラルステアに近い状態で4輪ドリフトしている写真(著書写真41)を掲載して、 ”これがコーナーを最も早く回るテクニックである”と記述。
1964年5月に行われた第2回日本グランプリでホンダS800を運転するF1レーサーのロニー・バック ナムが鈴鹿の第1,第2連 続コーナーをニュートラルステアの前輪はまっすぐ向けたまま、アクセルコントロールで4輪ドリフト状態で
サーカスのように毎回安定して周回していたのを今でも覚えています。
一般的にアンダーの強い市販車では、運転中にアンダーを感じたらカーブに高速で進入しないのが無難。
対照がラリー車の走り、絶対と言っていいほどスピンはしない。 先の読めないカーブに無理なスピードで突っ込んで行っても、横滑りしながらなんでも無いように走り去っていく。
弱めのアンダーステアではリヤには無理がかかって、横滑りによりカーブを通過する速度は遅くなってしまうが、フロントは自在でコントロールを失うことはない。 無理なカーブ進入でも減速するだけで、コースを飛び出すほどの極端なオーバースピードでない限り素人でも運転に失敗することは無い。
リバースステアについては4節の「リバースステア 強US車両の挙動」
および5節の「弱US車両の挙動」に.
今まで簡単な式で表せる車両運動逆モデルの働きについて述べてきましたが、ドライバモデルを構成する位置づけは下図のようになります。
車両運動逆モデルにより 行うべき 運動αからそのための操作δを生じる
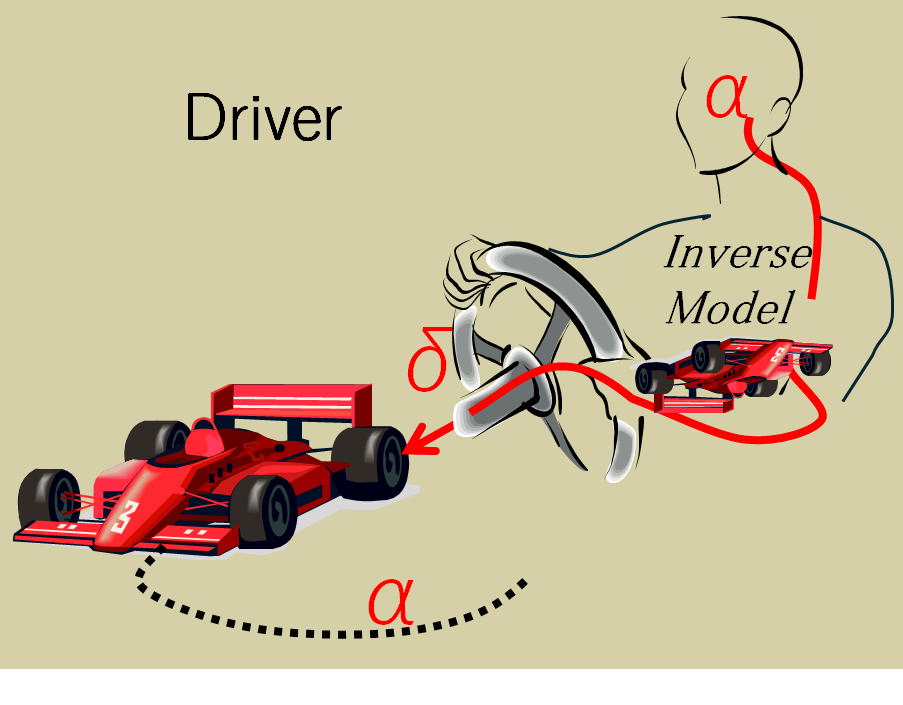
入力があってその結果出力が生じる、ハンドル操作があって車は曲がっていく。 ところが車の運転行為は一寸違う、最初に運動が頭の中に浮かぶ、例えば前のカーブを曲がろうとすると、最初にカーブでの自車の行うべき運動αが設定され、その為のハンドル操作δが頭の中に生じる。
すなわち結果である運動αから入力δが生じるのである。 その為には自分の中に、練習によって運動αから操作量δを生じる 対象車両の運動逆モデル(最初に記述の運動方程式) を獲得していなければ成らない。 逆モデルが正確ならこのδによって確実に思った運動αが実現できることになる。
車体と一体のリヤタイヤに働く力の加減には、 ステアリングからフロントタイヤに至る操舵系の運動特性およびこれによる車両の応答/運動特性など全てが、
十分な経験に基づいて身に付いて(身体に逆モデルがプログラムされて)いることが必要。
簡単な式で表せる逆モデルの行う見事なレーンチェンジの動画をもう一度見ていただきます。
逆モデル・AI ドライバーによるシビアなレーンチェンジ
車両はCarSim。
前後輪に発生する横方向の力を、路面に平行な黄色の矢印で示し、上下方向の力を路面に垂直な矢印で示す
最初にリヤタイヤに働く黄色の矢印を見てください。
リヤタイヤに働く力が、レーンチェンジに合わせて左に、右にと変化しているのが分かると思います。 先行するフロントタイやの力で車体の向きを変え、それによって発生するリヤタイヤのコーナリングフォースでレーンチェンジしている様子がよく分かる。
巧みなステアリング操作で前輪が発生する力をコントロールして車体の向きを変えて、車体とともに向きの変わるリヤタイヤにレーンチェンジする力を発生させているわけです。
さらに、自分も中に乗っていて慣性力を受けるので、不快にならないようどう力加減したらよいか、人の感覚特性に基づいた力加減の仕方を身につけている必要がある。