運転行為／Weber則関連

Forth　

運転関連

★ステアアシスト　運転アシスト

< id="SteerAssist">
Steer Assist （ステアアシスト）：ジャンプ元に戻る
　タイヤの能力限界まで意図した旋回を、逆ハン状態も含めて実現する。

　時々刻々の力のコントロールで積分時間を経て速度、変位が実現できる。
　運動のコントロールは実現すべき目標（速度、変位が）に、先行した計画的な力のコントロールで目標運動状態を実現する。

　すなわち運動加速度を計測すれば目指す運動が推定できる。

　走行中の車の横加速度αを車両運動逆モデルに代入して、その運動状態αにふさわしい操舵角δをこの逆モデルで計算する。
　もし現在の操舵角がこれと異なる場合は、その分を修正することになる。

　機械的にゆっくり　Fishhookターン（Jターン）を行なえるハンドル捌きの運転で速度を上げて走るとどうなるのか。

　速度を上げるとスピンしてしまう場合の、操舵支援を行った場合の走行シミュレーション動画を右に示す。　緑が支援なし、白が支援車。

　両車両は全く同じドライバによる全く同じステアリング操作でありながら、白のステアアシストされている車両では意図通りの滑らかな旋回を実現できているる。

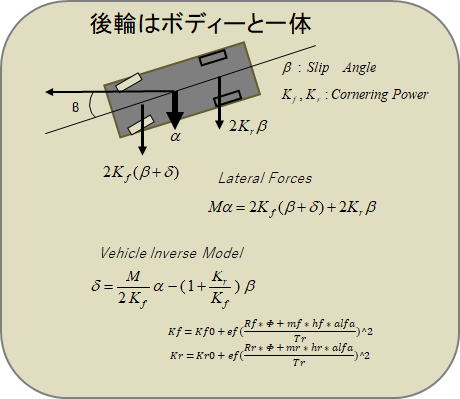
Kf=Kf0+εf ((Rf φ+mf hf α)/Tr )^2　　Kr=Kr0+εf ((Rr φ+mr hr α)/Tr )^2
（δ:操舵角、m,mf,mr：質量　Kｆ、Kｒ：前後タイヤのコーナリングパワ　εf ：荷重依存係数　α：横加速度　φ:ロール角 hf,hr：前後ロールセンタ高　Rｆ、Rｒ:前後ロール剛性　β：車体横滑り角(実車から得る)）

車両は CarSim(Mechanical Simulation社）　
運動逆モデルは　MATLAB/Simulink　で作成

★ 車の運転の成り立ち・仕組み：　車両適合＋環境適合＋感覚生理適合

・一点注視　像を網膜に固定：　Adapt to Vehicle Dynamics
　ピッチング（常時）、ヨーイング（横滑り時は特に）を首・眼球の動きで補正して常に一点注視で網膜上の像を固定する

・前方環での運動状態を決定：　Adapt to Traffic Environment
　前方環境位置、通過速度の決定。　見込み運動のパラメータ決定。

・車両特性に沿う： Adapt to Vehicle Dynamics
　車両入出力特性に従った機械的な操作

・感性に沿う：Adapt to Sensory/Motor
　感性に沿った力のコントロールで滑らかに運動状態を実現する

★ 感覚に沿った操縦系インターフェース例：
　高減速度でも踏んだら踏んだだけ効く、感性に忠実なブレーキ

　私たちは顕微鏡の世界から宇宙まで、家計簿から国家予算まで、小さな刺激から大きな刺激まで実用的に受け入れる。
　効き具合が機械的な線形では非常に狭い範囲の物理量しか人間の感覚に合わせられない。
　ブレーキの利きは、0.3G付近が丁度良い効き具合になっているようだが、0.1Ｇ以下の低いＧのところではもっと微調が効いて欲しいし、 0.3G付近の利きのまま線形外挿しした高Ｇの所では効きが物足りなくなってしまう。

　 Drive by Wire（ドライブ　バイ　ワイヤ）：
　生理学上の法則であるWeber（ウェーバー）の法則に従って、操作側の特性と応答側の特性を、人にとって感覚上線形に対応させる。

　右図示すように、感覚上線形とは操作量の踏力と応答加速度の関係がべき乗に成るべきとWeber則は言っている。
　大抵は操作する手足のWeber比　Cf　の方が身体を支えるWeber比　CF　より小さいので、応答曲線は下に凸の関数になる。

　踏力-減速度で表すブレーキの特性を例にとると、感覚上良く効くブレーキでは右図に示すよう、下に凸の２次曲線（実際は1.?次）のような形になるべきを、一般の車のブレーキは構造上直線なので、感覚的な期待に対しては踏むほど、踏力の大きい所ほど感覚的には効かないブレーキとなる。
　ブレーキの効く効かないは感覚でしかないので、実際効かないのである。　踏力の大きいところでは感覚的な期待に対しては効かないブレーキとなるので、強く効かすときはガンと踏めとなってしまう。

　宇宙一良く効くと言われるポルシェのブレーキは、踏力-減速度で表すブレーキの特性は一般車と同じ直線だが、これを原点近くに急勾配で立てることによって、感覚上線形の曲線を沿わせてもこの曲線からあまり離れない形になっている。

　例えば、操作物理量ｆ、系の応答物理量F、各のWeber比をCf、CF（車の場合は身体を支える筋肉の調整能力で５％前後）とすれば、線形な　ｆ　と　F　の関係式は、操作量ｆの最小操作量Δｆに対して、その応答量が応答量Fの最小量ΔＦに成っていれば良いので、
　　dF/df*Δｆ=ΔF　
これにΔf=f*Cf　　ΔF=F*CF　を代入して積分すれば

　 F=K*ｆ^CF/C^f 　（べき乗関数）　　　　　　　　K　：は定数

　この関係式で操作量ｆと応答量Fが表せれば感覚上ｆとFは線形。

★ 人の制御則　x" = a - C x'　の応用

人は、地上では車、空では超音速飛行機、海の上では何万トンもの船を自在に操る制御能力を持つ。

交通環境に沿った走行例は下の動画
交通環境に沿った制御式の作り方ここをクリック

★ 滑らかで快適な運転＝安全運転

　段差に気が付かなければ足を踏み外す。見かけより重くても軽くても物は巧く持ち上げられない。
　滑らかに運転できたとは、ちゃんと先を読みきったこと。　滑らかさは安全運転の尺度になる。
　
　感性に沿って滑らかな運動を行う　　x" = a - C x'　　　この運動方程式も、前方環境での見込み運動状態量（位置、速度）が入力されて、初めて思った滑らかな運動を開始できる。
　前方環境を正確に読んで、滑らかな動きを実現できていると言うことは、この運動方程式に乗って動いていると言うことで、前方交通環境の把握が正確にタイミング良く行われている証拠。
　即ち運転の滑らかさが、安全運転度合いの尺度になる。　滑らかな運転ができる人ほど環境適合度合いが高い、すなわち安全となるわけです。

　人の運動制御方程式に前方環境の運動状態（位置、速度）を機械的に与えれば滑らかな見込み自動運転も可能。　平尾先生の言われる、前方環境の運動状態（位置、速度）に見込み違いさえなければ、名人の運転で快適にしかも安全に運んでもらえる。（中嶋悟の上手い運転とは）